Fourth grade really focuses on cementing the idea that fractions are parts of a whole that can be added together or broken apart. Students work solely with like denominators to add, subtract, model, write equations, and justify their thinking. Students should be able to do this with mixed numbers and fractions and be able to use visuals to solve word problems. How do I accomplish all of that you ask?
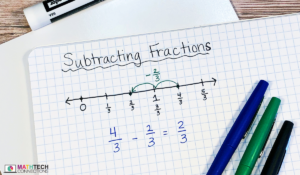
Adding Fractions With Like Denominators
Pattern blocks and number lines are ideal for fourth graders because they provide consistent denominators.
When using pattern blocks, students can substitute shapes for fractional names. 1 rhombus + 2 rhombuses = 3 rhombuses. Since a rhombus represents one third, students can replace “rhombus” with “third” to show addition. 1 third + 2 thirds = 3 thirds.
Number lines are great too, and it’s okay if students aren’t precise as they divide their number lines. Grid paper will help keep their work neat, but it’s not necessary. In this example, you can see how number lines can also show how fractions can add up to more than one whole.
Subtracting Fractions With Like Denominators
Keep those pattern blocks out for subtracting fractions. Students who struggle will appreciate being able to use pattern blocks to build a fraction, then take away piece by piece to subtract and see what’s left over. Here we start with 5/6 and subtract 3/6, to show 2/6 left.
Some students will also benefit from counting back on a number line to show how to subtract. When you start with 1 1/3, and need to subtract 2/3, some students will get stuck, since they don’t have 2/3 to subtract. When using a number line, they can count back 1/3 at a time to show 2/3 remaining.
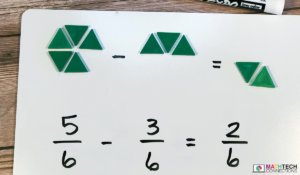
Solving Word Problems Like a Pro
The key to solving word problems is to make sure you really understand what the question is asking. If a student can’t explain the problem without looking at it, he probably doesn’t understand it well enough to solve it…yet. Rereading the problem and drawing a picture are invaluable tools for success.
Here’s an example of how you can support your students’ understanding of fractions with word problems. There’s an expectation that students model and explain their thinking.
Additional Activities to Add and Subtract Fractions:
Leave a Comment