In the previous blog post, we talked out how the compensation strategy can help students create simpler addition problems, you can view the blog post about it here.
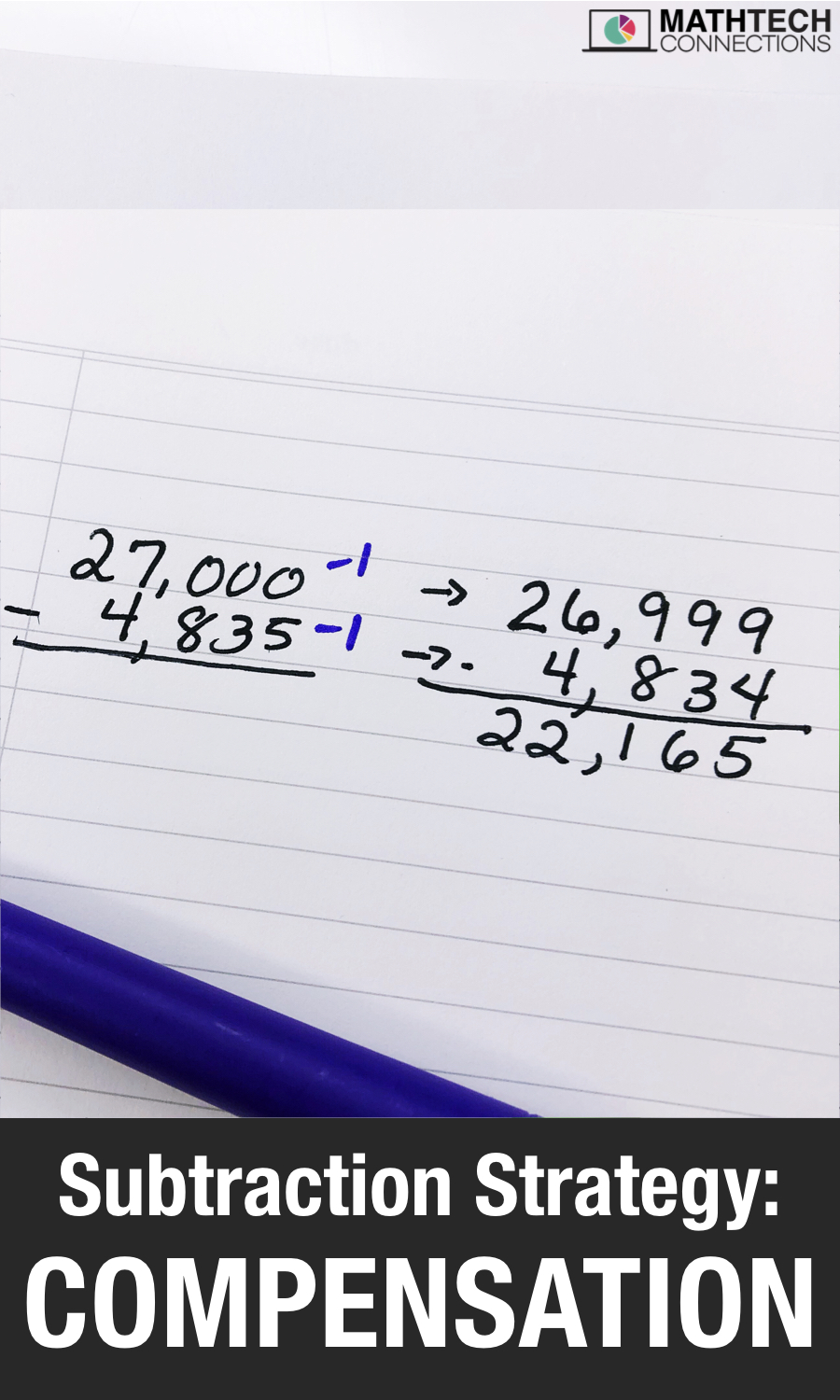
Today, let’s look at how this strategy works in subtraction.
Example 1: 800 – 254
- You take 1 from 800 and get 799
- You then take 1 away from 254 and get 253
- The new expression is 799 – 253
Both expressions equal 546, but the second expression (799 – 253) is simpler to solve because students don’t have to subtract across zeros.
WHY DOES THIS STRATEGY WORK?
Let’s look at some vocabulary words.
minuend – subtrahend = difference
The subtrahend is the amount you are taking away from the minuend. When we took 1 away from both the minuend (800) and subtrahend (254), the difference stayed the same.
Why?
We didn’t change the distance between the numbers. We simply shifted the numbers on a number line (see example #2).
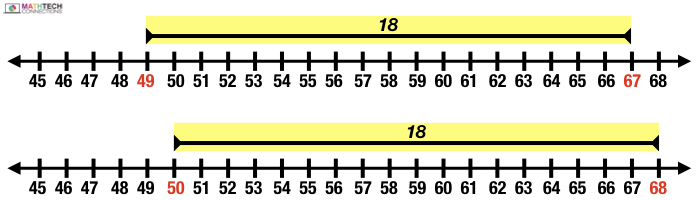
Example 2: 67 – 49
- You add 1 to the minuend (67) and get 68
- You then add 1 to the subtrahend (49) and get 50
- The new expression is 68 – 50
Both expressions equal 18, but the second expression (68 – 50) is simpler to solve since students don’t have to regroup. In this example, we added 1 to the minuend and subtrahend. The difference (distance between the numbers) stayed the same.
MORE EXAMPLES
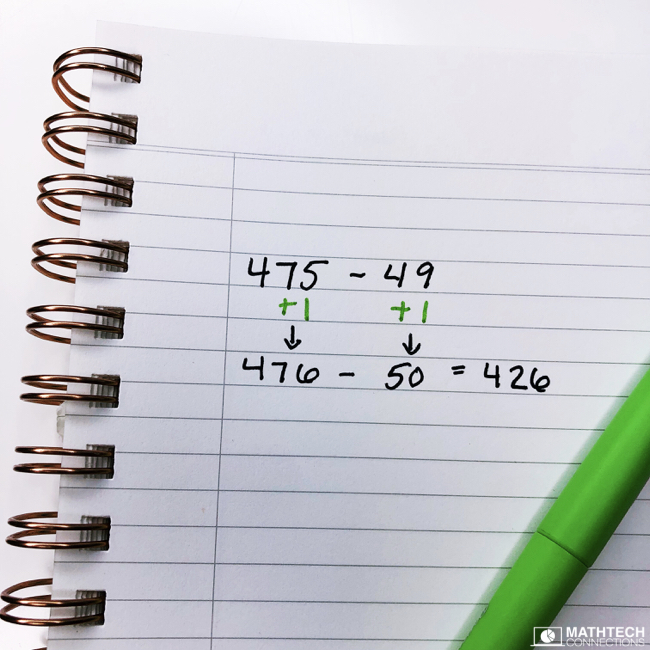
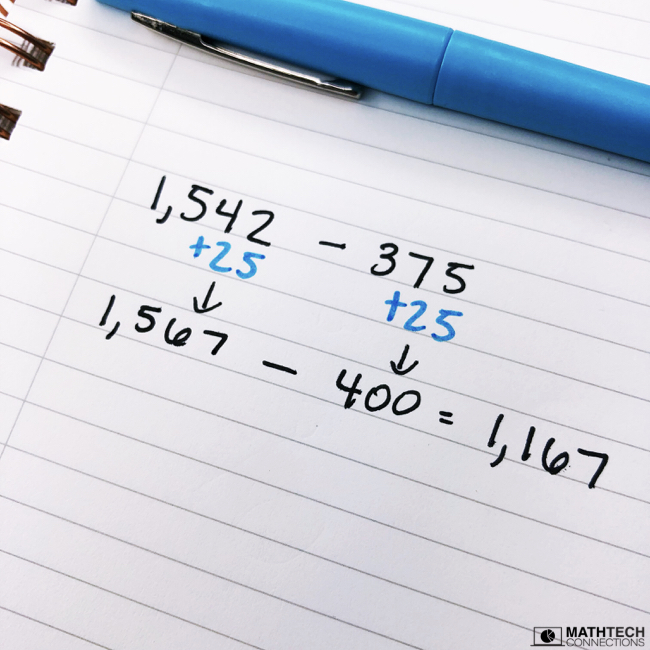
Up Next…
In next week’s email, I’ll share with you how students can use base 10 blocks and place value disks to model addition and subtraction problems. You don’t want to miss the freebie that’s included!
SHOP PLACE VALUE RESOURCES
 Add to Cart |
 Add to Cart |
 Add to Cart |
 Add to Cart |
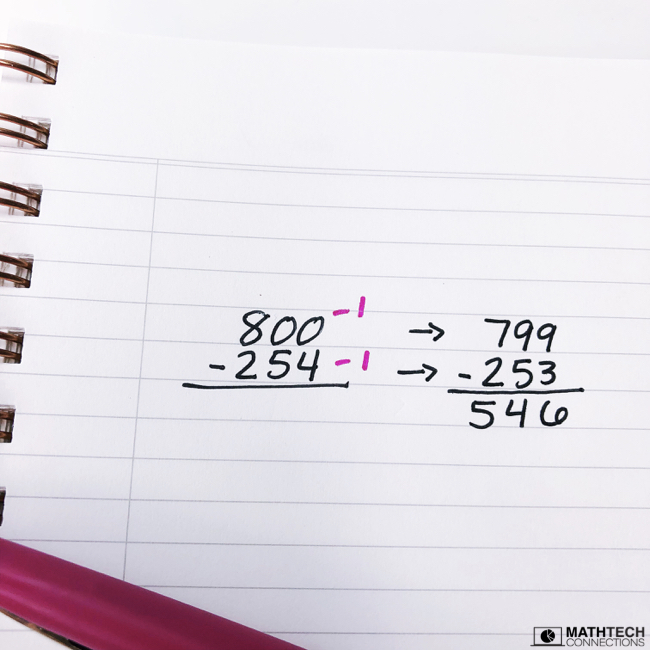
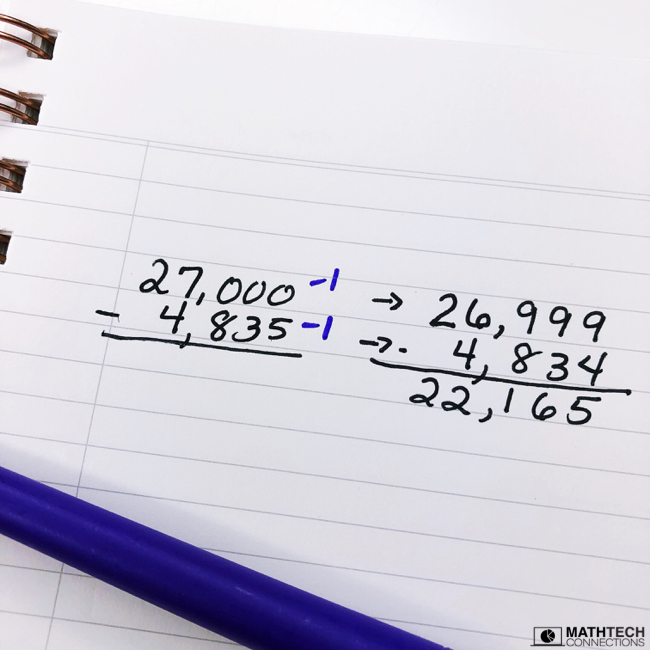
Thank you for sharing. I know this will help my struggling students.