
I will admit, I disliked teaching fractions. It was a topic that students struggled to understand, and I found myself frustrated as I followed the book.
I made it my goal to not feel that way again. I searched online and found an amazing resource that every teacher needs to read!

This book literally changed how I taught fractions. I no longer needed to follow the book, because I understood how students build their understanding of fractions.
If you teach grades 3-5, you need to get yourself a copy.
Let’s talk about comparing fractions
Teaching fractions can be hard, and students will need plenty of opportunities to explain their thinking.
Students begin by explaining their thinking using drawings. Their drawings can be in the form of area models or models on a number line.
Students will then need other strategies as they move from a concert understanding to an abstract understanding of fractions.
Below are 4 strategies students can use to explain their thinking as they compare fractions. A free download is located at the bottom of this blog post.
- Fractions with the same numerator
- Fractions with the same denominator
- Use the benchmark number 1/2
- Use the benchmark number 1

Fill out the form & the freebie will be sent to your inbox!
Strategy #1: Fractions with the Same Numerator
When the numerators are the same, we know that we have the same number of pieces.
– Example: 2/3 and 2/6
Each fraction is referring to two pieces, but the pieces are different sizes. Two-thirds is referring to larger pieces. Two-sixths is referring to smaller pieces.
Two-thirds is greater, because it’s referring to two larger pieces. Students can explain their thinking further by stating that sixths are smaller because the whole has been cut into more pieces. The more you cut a whole, the smaller the pieces get

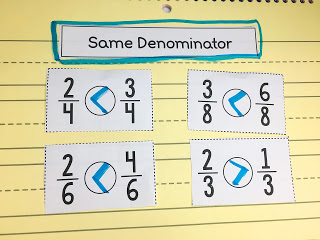
Strategy #2: Fractions with the Same Denominator
When the denominators are the same, we know that we are talking about pieces that are of equal size.
– Example: 1/4 and 3/4
Each fraction is referring to different number of pieces, but the pieces are of equal size. One-fourth is referring to one piece. Three-fourths is referring to three pieces.
Three-fourths is greater, because it has more of the equally-sized pieces.
Strategy #3: Use the Benchmark 1/2
When fractions don’t have the same numerator or denominator, it helps to compare the fractions to 1/2.
– Example: 3/6 and 5/8
Each fraction is referring to different numbers of pieces, and the pieces are different sizes. I do know that three-sixths is exactly 1/2.
Five-eighths is greater than three-sixths, because 5/8 greater than half. Students can explain their thinking further by stating that 4/8 is half, so 5/8 is greater than half.

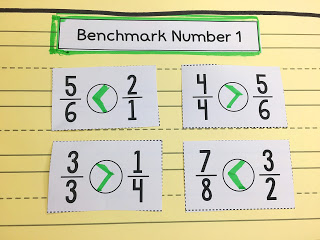
Strategy #4: Use the Benchmark 1
You can compare fractions by looking for fractions that are close to one, equal a whole number, or looking for improper fractions.
– Example: 6/6 and 7/8
Each fraction is referring to different numbers of pieces, and the pieces are different sizes. I do know that 6/6 equals one. Seven-eighths is less than one.
Six-sixths is greater than 7/8, because 6/6 equals one.
– Example: 3/4 and 5/6
Each fraction is referring to different numbers of pieces, and the pieces are different sizes. I do know that each fraction needs one more piece to equal one. Sixths are smaller than fourths, so 5/6 is missing a smaller piece in order to make a whole.
Five-sixths is greater than 3/4, because it is closer to a whole.
– Example: 2/3 and 3/2
Each fraction is referring to different numbers of pieces, and the pieces are different sizes. I do know that 2/3 is less than one. Three-halves is greater than one.
Three-halves is greater than 2/3, because 3/2 is greater than one. Students can explain their thinking further by stating that 3/2 is equivalent to one and one-half.
Free Comparing Fractions Printables for Your Classroom
Fill out the form below to download the FREE printable pages and use them in your classroom. You will find example problems for your students to practice each strategy.

Fill out the form & the freebie will be sent to your inbox!

Save paper by placing this larger version in a sheet protector.
















Leave a Comment