
I am sure many of you will agree that looking at the common core math standards can be confusing at times. I have decided to start a new blog series where I will do my best to look at each standard and explain what it means, what it looks like, and how to best teach it to students so they will build a deep understanding. I’ve taught third grade for 5 years and am still learning, so please do comment with your opinions.
Let’s start by looking at the fractions domain. The first standard is 3.NF.1…
Confusing, right? So, what I understand from this is that students need to know that a fraction is made when a whole is broken/cut/partitioned into equal parts. Each part is a fraction of the whole. It’s best if students start learning about fractions by using equal sharing problems. See the examples below…

It is during this time that we start talking about what partitioning means and how important it is for each piece to be of equal size. We make sure that when we are partitioning the circles/rectangles (cookies/pies/bars) that the pieces are all the same size.
Let’s look at problem one. Students will say Amy and Olivia each get one piece each. This is when we start talking about how each piece has a special name. They cut the cookie in half, so each student gets….”one half”. We then move on to problem two where Isabela, Brandon, and Carlos each get one out of three pieces or “one third”. In problem three, the friends get one out of four pieces or “one fourth”.

This is a perfect time to create an anchor chart that will display fractions using area models. It seems very simple, but some students will be confused as to how you can ‘cut’ a circle, rectangle, or square into equal parts unless they have plenty of practice. Students can copy the anchor chart inside their math notebook, so they can refer to their mini-anchor chart as needed. Below is a mini-anchor chart I drew in a notebook.
The following question can be used as an exit ticket to see if students have an understanding of equal parts.
If students do not do well on this exit ticket they need extra practice partitioning circles, squares, and rectangles. You will find a practice sheet in the free download at the end of this post.
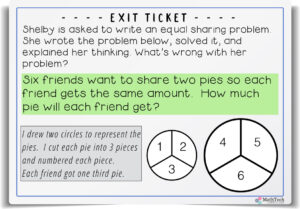
When students have mastered equal sharing problems that involve one item I move on to sharing problems with more than one item. It is very important that students understand the items that are shared must be the same size and shape. Look at the examples & exit ticket below.


Students think it’s fun when there is more than one way to find the answer, so I make sure the groups have time to share how they solved he problems. Again, this is a good time for students to practice naming each part. For example, in problem one, one group might say that each friend gets one half pizza and another group might say each friend gets two fourths pizza. This is a good time to discuss how one half and two fourths are the same. In problem two, each friend gets two thirds chocolate bar. In problem three, each friend gets two sixths or one third pizza. In problem four, each friend gets three fourths chocolate bar. Below is an example exit ticket to give students.
This exit ticket should bring an interesting conversation from students. Yes, both pies are cut into thirds, but the friends will not get the same amount of pie. One pie is larger than the other, so three friends (4-6) will actually get more pie. After going through these two levels of equal sharing problem and practicing writing fractions in words, I begin introducing how to write fractions using numbers.
When introducing how to write a fraction using numbers, I focus A LOT on talking about how many pieces are in the whole. This is a good time to bring out the pattern block shapes. Look at the problems below.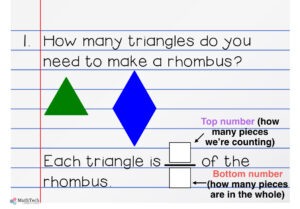
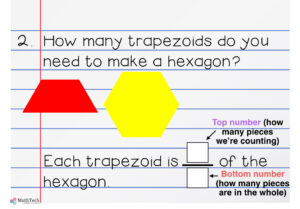
In problem two, students will find out that 2 red pattern block trapezoids make a yellow hexagon. So, each red trapezoid is one half of the hexagon. The top number is how many trapezoids we’re counting (one) and the bottom number is how many trapezoids make up the whole (two).
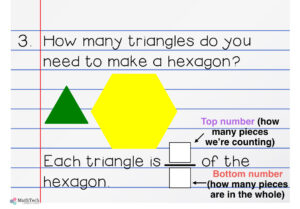
In problem three, students will find out that 6 green pattern block triangles make a yellow hexagon. So, each green triangle is one sixth of the hexagon. The top number is how many triangles we’re counting (one) and the bottom number is how many triangles make up the whole (six).
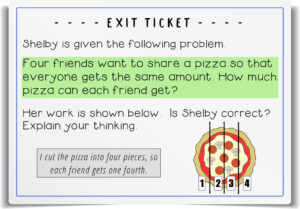
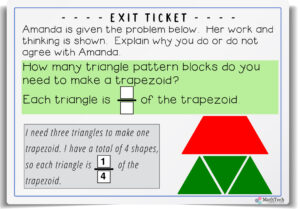
This little exit ticket will let you know if students are understanding the parts of a fraction. Amanda is incorrect in her thinking of the bottom number. The trapezoid is made up of three triangles, so the bottom number needs to be three. Each triangle is one third of the trapezoid.
I am actually going to stop here for today. WOW! There is a lot to learn about representing fractions using area models. 🙂 You can download a free copy of problems used in this blog post at the end of the article.
Download the Fraction Bundle!
Enter your email address and receive the free fraction bundle today!

















I really enjoyed your post about the standards for fractions. As a preservice teacher, I have spent a good amount of time looking into standards for different subjects and think it is a good idea to lay out what the students are doing in your classroom for the students’ parents/ guardians. This helps to rationalize what you are doing in the classroom as well as helps parents/guardians to help their students at home. The more the parents understand, the better their help will be. I really like how you have laid out what students might say in response to a question that they are working on. Through my clinicals, I have learned that having these misconceptions laid out is extremely beneficial for planning because it makes it easier for you as a teacher to come up with a response.
Van de Walle (2014) states that students would better understand fractions if there were more emphasis across the different meanings or interpretations of fractions (part-whole relationship, measurement, division, operator, and ratio). The one thing I would say to add to your blog is different ways of looking at fractions. I did not see any number lines where students could place fractions or looking at fractions as ratios.
Van de Walle, J.A., Lovin, L.H., Karp, K.S., & Bay-Williams, J.M.
(2014). Teaching Student Centered Mathematics: Developmentally
Appropriate Instruction for Grades 3-5. Saddle River, NJ: Pearson.
Thank you so much for your kind words! It was my goal to make a ‘part 2’ and talk about fractions on a number line, but I haven’t had the free time to do this yet. By the way – I have your book and LOVE it! It’s one of the first books I looked at when starting math workshop in my classroom 🙂
My district has purchased Wonders by McGraw Hill as our new reading series. I searched Pinterest for any 3rd grade materials and found several that I pinned. When I try to find them I am directed to this blog and all I see are math ideas and materials…. Help! Where do I find the Wonders items you’ve made?
Please email me at mathtechconnections @ gmail . com
thank you for offering your fraction bundle. I am experiencing some difficulty in locating it, however. Your blog directs me to list my email and then to confirm my subscription. I have checked all my boxes and cannot see an email in return from you to confirm the subscription. Hence, no fraction bundle is forthcoming. Is there another way I can access it? thanks a bunch!!
Thanks so much!! Your blog and download are so user friendly. I’m looking forward to using them with my enrichment second graders next year.
Thank you so much!! I was thinking about putting this together – I started gathering information but STOPPED because it was time consuming. BUT you made my day.. Thank you.
You are so welcome 🙂 Happy to help!