Symmetry is a geometric attribute where a shape or object contains one or more mirror images when divided in half. This means that when the shape is folded in half the halves match up perfectly. A line of symmetry is called a line of reflection.
MA.3.GR.1.3 – Draw line(s) of symmetry in a two-dimensional figure and identify line symmetric two-dimensional figures.

Understanding Symmetry
Symmetry is a skill in preparation for more advanced geometric skills quite a way down the line (8th grade!). At the same time, it is a helpful concept for understanding area models of fractions and equal partitions.
The reasoning can be divided into two levels:
a.) Can the shape be divided into two equal halves? You can see the rectangle to the right is divided into two equal halves.
b.) Are the halves symmetrical? The diagonal line across the rectangle is not a line symmetry. If the rectangle were folded, the halves would not line up perfectly. The rectangle does have a vertical and horizontal line of symmetry, though.

In 3rd grade, students progress from identifying line-symmetric shapes to understanding that figures may not be symmetrical or may have 1 or more lines of symmetry.
Sometimes it’s Tricky…

By far the best way to begin to develop symmetrical understanding is by folding shapes printed on paper.
Students should have plenty of experience with examples and non-examples of symmetrical shapes.
They can then begin to examine divided shapes like the H to the left, and finally start dividing shapes themselves.
Some shapes are trickier than others!
Like the example of the rectangle earlier, capital letters N, S, and Z have attributes that students may perceive as symmetry. Upon further inspection, none of these letters are symmetrical because their component lines reverse direction.
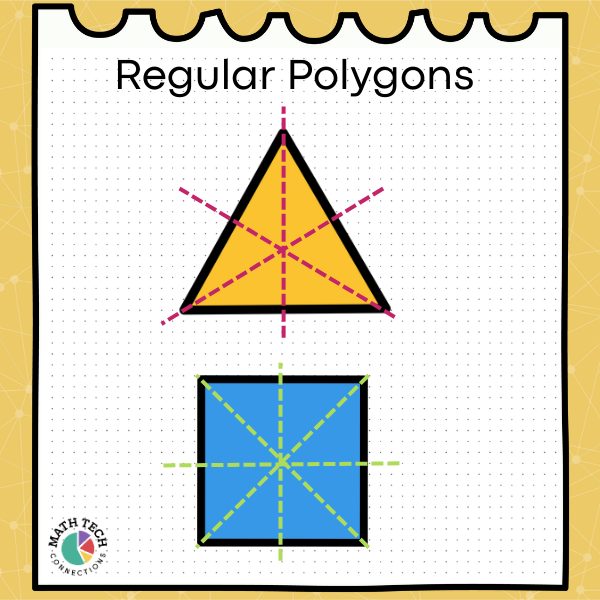
Regular Polygons
Some shapes are obviously not symmetrical, and some need to be tested for lines of symmetry. Regular polygons, like equilateral triangles and squares, have lines of symmetry equal to their number of sides.
Equilateral triangles have three lines of symmetry, squares have 4 lines of symmetry, and so on.
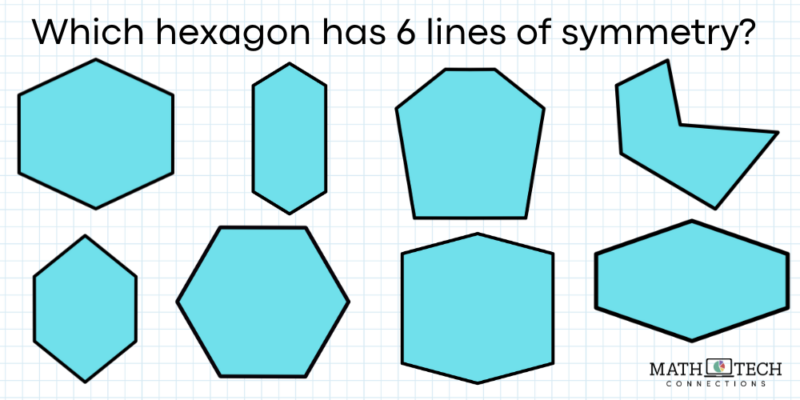
It can be fun (and reinforce geometric understanding of attributes of polygons) to examine different representations of shapes in the same category, like hexagons, to compare and contrast their symmetrical attributes. Hexagons can have 6 lines of symmetry, 2 lines, 1 line, or none at all.
Standards
Florida’s B. E. S. T. standards introduce symmetry considerably earlier than Common Core and TEKs, which both address the concept in 4th grade. 3rd grade is already a packed year of mathematical study, but symmetry can easily be combined with geometry and/or fractions. It is a fun way to add another layer of geometric reasoning to your geometry and fraction study!


















Leave a Comment