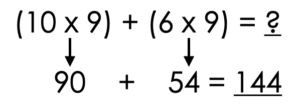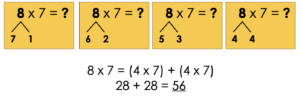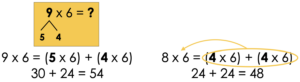The distributive property is helpful for breaking down difficult problems!
It says a factor in a multiplication equation can be broken into 2 addends. Essentially, you end up solving 2 easier equations and adding to get the product.
Here is an example:
16 x 9 = ?
We can break up either factor.
16 is big, so let’s break it up!
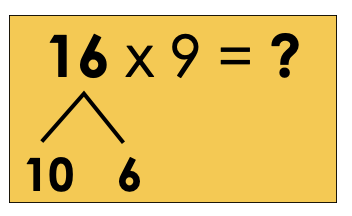
You can break 16 into any 2 addends, as long as the whole number gets multiplied by 9.
We can try 10 and 6.
Our equation turns into a multi-step equation.
(10 x 9) + (6 x 9) = ?
Using the new equation, what is the product of 16 x 9?
16 x 9 = 144
The distributive property does add a couple of steps, but we can use easier facts to solve more difficult problems.
Use the distributive property to break up the 8 in 8 x 7 to make an easier, multi-step equation to solve.
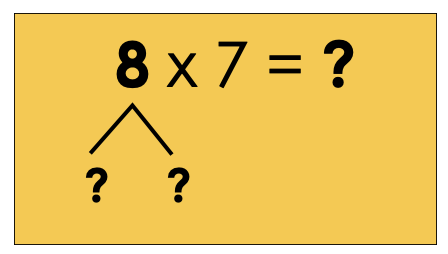
Did you get 56?
You can break into any 2 addends:
Remember, the parentheses tell us which parts of the equation to solve first.
The distributive property is often used with arrays.
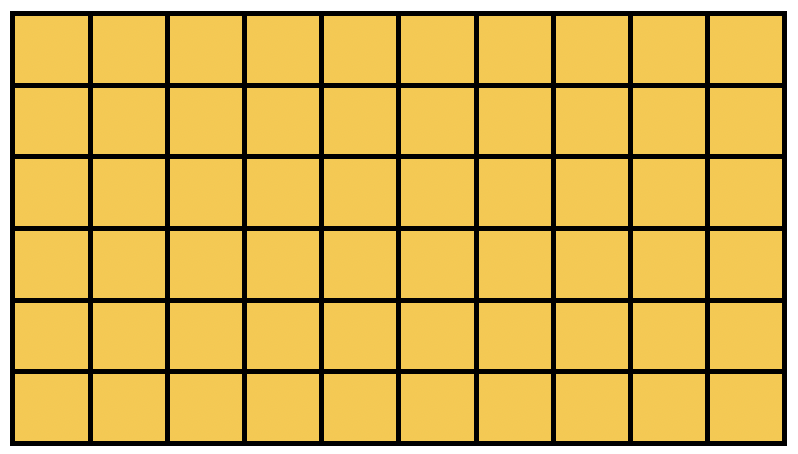
This array illustrates 6 rows of 10 or 10 x 6.
How can you break up one factor in 10 x 6 to create 2 easier expressions?
There are many ways to break 10 x 6 into smaller parts!
- (10 x 3) + (10 x 3) = 60
- (10 x 4) + (10 x 2) = 60
- (5 x 6) + (5 x 6) = 60
- (7 x 6) + (3 x 6) = 60
- (8 x 6) + (2 x 6) = 60
Practice Problems
True or False?
15 x 6 = (10 x 5) + (5 x 6)
50 + 30 = 80
True or False?
8 x 8 = (8 x 4) + (8 x 4)
32 + 32 = 64
The 2nd equation above does NOT multiply the whole 9 times 6!
4 + 4 = 8 so the two sides of the equal sign are not equivalent.